Dividiendo un círculo en 6 partes iguales: Guía completa

La necesidad de dividir un círculo en partes iguales surge en diversos ámbitos, desde la geometría básica hasta la arquitectura o el diseño. Ya sea para crear un diagrama, un logotipo o un patrón, la habilidad de dividir un círculo en 6 partes iguales es una herramienta valiosa.

En este artículo, te guiaremos paso a paso a través del proceso de dividir un círculo en 6 partes iguales, explorando diferentes métodos y aclarando cualquier duda que puedas tener.

Puntos Clave

• Método básico para dividir un círculo en 6 partes iguales
• Uso de un compás para mayor precisión
• Aplicaciones prácticas de dividir un círculo en 6 partes iguales
• Relación con ángulos y medidas
• Variaciones y extensiones del método básico
• Utilidad en geometría, diseño y arte
• Ejercicios y ejemplos prácticos
• Recursos adicionales para aprender más

Método básico para dividir un círculo en 6 partes iguales

Este método se basa en la construcción de un hexágono regular dentro del círculo.

1. Trazar un diámetro: Comienza trazando una línea recta que pase por el centro del círculo, conectando dos puntos opuestos en la circunferencia. Esta línea representará uno de los lados del hexágono.
2. Dividir un semicírculo: Con el centro del círculo como punto de referencia, traza dos líneas adicionales que dividan el semicírculo (la mitad del círculo que contiene el diámetro) en tres partes iguales.
3. Extender las líneas: Extendiendo estas dos líneas hasta que crucen el diámetro en el lado opuesto del círculo, completarás la construcción del hexágono regular. Las líneas ahora dividen el círculo en seis partes iguales.

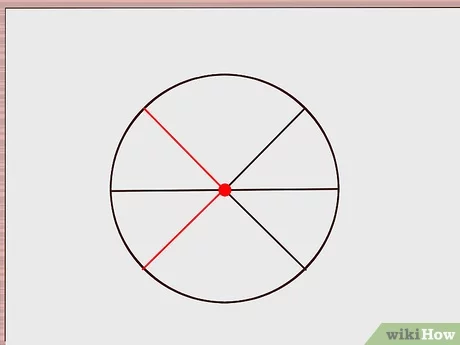
Visualización del método

Puedes visualizar este método usando un diagrama simple. Imagina un círculo y su diámetro, dividiendo el círculo en dos mitades. Ahora imagina dos líneas adicionales que se originan en el centro del círculo y se extienden hacia el borde del círculo, dividiendo cada mitad en tres partes iguales. Si extiendes estas líneas a través del diámetro, crearás un hexágono regular dentro del círculo.

Utilizando un compás para mayor precisión

Si necesitas una mayor precisión en la división del círculo, puedes utilizar un compás.

1. Ajustar la abertura del compás: Ajusta la abertura del compás al radio del círculo (la distancia desde el centro del círculo hasta cualquier punto en la circunferencia).
2. Marcar puntos en la circunferencia: Con el compás ajustado, coloca la punta seca en el punto donde el diámetro interseca la circunferencia. Traza un arco en la circunferencia del círculo, marcando un nuevo punto. Repite este proceso, usando el nuevo punto como centro, hasta que hayas marcado seis puntos alrededor de la circunferencia.
3. Unir los puntos: Conecta los seis puntos con líneas rectas. Estas líneas formarán un hexágono regular inscrito en el círculo, dividiendo el círculo en seis partes iguales.

Beneficios de utilizar un compás

Utilizar un compás te permite garantizar que la división del círculo sea precisa y simétrica. La apertura constante del compás asegura que todos los segmentos del hexágono tengan la misma longitud, lo que resulta en una división del círculo en seis partes iguales perfectas.

Aplicaciones prácticas de dividir un círculo en 6 partes iguales

La habilidad de dividir un círculo en 6 partes iguales es útil en diversas aplicaciones:

• Diseño gráfico: Diseñadores gráficos pueden utilizar esta técnica para crear logotipos, patrones o elementos gráficos basados en formas hexagonales.
• Arquitectura: Arquitectos pueden usar esta técnica para diseñar estructuras con elementos circulares y hexagonales, o para calcular el espacio necesario para áreas circulares.
• Ingeniería: Ingenieros pueden utilizar esta técnica para diseñar sistemas de engranajes o sistemas mecánicos que requieran componentes hexagonales.
• Artesanía: Artesanos pueden utilizar esta técnica para crear objetos con formas hexagonales, como mosaicos o objetos de cerámica.

Relación con ángulos y medidas

Cada una de las seis partes iguales en las que dividimos el círculo forma un ángulo central de 60 grados. Esto se debe a que la suma de los ángulos alrededor de un punto es 360 grados, y dividiendo 360 grados entre 6 partes iguales obtenemos 60 grados por parte.

Conceptos geométricos relacionados

La división de un círculo en 6 partes iguales está directamente relacionada con la geometría de los hexágonos regulares. Un hexágono regular tiene seis lados iguales y seis ángulos iguales, y cada ángulo interior mide 120 grados. La relación entre los ángulos del hexágono y los ángulos del círculo dividido en 6 partes iguales es fundamental para entender la construcción de este proceso.

Variaciones y extensiones del método básico

El método básico de dividir un círculo en 6 partes iguales se puede adaptar para crear otras divisiones:

• División en 12 partes iguales: Dividiendo cada una de las 6 partes del círculo en 2, se obtiene un círculo dividido en 12 partes iguales.
• División en 3 partes iguales: Trazando un diámetro y un tercer punto en la circunferencia equidistante de los extremos del diámetro, se crea un triángulo equilátero inscrito en el círculo, dividiendo el círculo en 3 partes iguales.

Aplicaciones de las variaciones

Estas variaciones del método básico pueden ser útiles en diferentes aplicaciones. Por ejemplo, la división en 12 partes iguales se puede utilizar para crear un reloj circular, mientras que la división en 3 partes iguales se puede utilizar para crear un logotipo con tres segmentos.

Utilidad en geometría, diseño y arte

La habilidad de dividir un círculo en 6 partes iguales es fundamental en muchos campos:

• Geometría: Proporciona una base para entender la construcción de figuras geométricas, como hexágonos regulares y triángulos equiláteros.
• Diseño: Facilita la creación de patrones, logotipos, diseños de productos, y otros elementos gráficos.
• Arte: Se utiliza para crear mosaicos, mandalas, y otras obras de arte que incorporan formas geométricas.

Ejemplos de aplicaciones

Ejemplos de aplicaciones de la división de un círculo en 6 partes iguales se pueden encontrar en las siguientes áreas:

• Diseño de logos: Muchos logotipos usan formas hexagonales, lo que implica la división de un círculo en 6 partes iguales.
• Creación de mosaicos: Los mosaicos de forma hexagonal se basan en la división de un círculo en 6 partes iguales, creando patrones complejos y atractivos.
• Construcción de estructuras: Algunos edificios y estructuras utilizan elementos circulares y hexagonales, lo que implica la comprensión de la división de un círculo en 6 partes iguales.

Video Recomendado: Dividiendo un círculo en 6 partes iguales: Guía completa

Preguntas Frecuentes

¿Puedo dividir un círculo en 6 partes iguales sin usar un compás?

Sí, puedes dividir un círculo en 6 partes iguales sin usar un compás, aunque la precisión del método puede ser menor. Puedes utilizar una regla y un lápiz para trazar el diámetro del círculo, y luego estimar la posición de los puntos en la circunferencia que dividan el círculo en seis partes iguales.

¿Cómo puedo dividir un círculo en 6 partes iguales con un ángulo de 60 grados cada una?

La división del círculo en 6 partes iguales forma automáticamente ángulos de 60 grados en cada sección. Cada sección del círculo tiene un ángulo central de 60 grados, ya que 360 grados (el ángulo total de un círculo) dividido por 6 partes iguales es igual a 60 grados.

¿Qué otras formas puedo dividir un círculo en partes iguales?

Además de dividir un círculo en 6 partes iguales, puedes dividirlo en otras cantidades de partes iguales utilizando diferentes métodos. Por ejemplo, puedes dividir un círculo en 4 partes iguales usando dos diámetros perpendiculares, o en 8 partes iguales usando cuatro diámetros perpendiculares.

Conclusión

Dividir un círculo en 6 partes iguales es una habilidad útil en muchos campos. Dominar este proceso te permite crear diseños, patrones, y objetos geométricos precisos. Puedes utilizar el método básico con una regla y un lápiz, o puedes optar por un compás para mayor precisión. Recuerda que la comprensión de los conceptos relacionados con los ángulos, los hexágonos regulares y los triángulos equiláteros te ayudará a comprender mejor la construcción de esta técnica.

Si quieres conocer otros artículos parecidos a Dividiendo un círculo en 6 partes iguales: Guía completa puedes visitar la categoría Educación.