Cómo calcular el área de un pentágono regular: Una guía completa

Los pentágonos regulares son figuras geométricas fascinantes que se encuentran en diversas aplicaciones, desde la arquitectura hasta el diseño. Calcular su área es una habilidad fundamental en geometría, pero puede parecer complejo a primera vista. En este artículo, exploraremos los diferentes métodos para encontrar el área de un pentágono regular, desde los conceptos básicos hasta las fórmulas avanzadas.

Aprenderás a determinar what is the area of the regular pentagon below, utilizando diferentes enfoques, y comprenderás cómo aplicar estos conocimientos en la práctica.

Puntos Clave

• Un pentágono regular tiene cinco lados iguales y cinco ángulos iguales.
• El área de un pentágono regular se puede calcular utilizando diferentes métodos, dependiendo de la información disponible.
• La fórmula más común para calcular el área de un pentágono regular es: Área = (5 * lado^2) / (4 * tan36°).
• El apotema es la distancia perpendicular desde el centro del pentágono hasta uno de sus lados.
• El radio es la distancia desde el centro del pentágono hasta uno de sus vértices.
• Puedes utilizar la trigonometría para determinar el apotema o el radio de un pentágono regular si solo conoces la longitud de sus lados.
• La fórmula para el área de un pentágono regular utilizando el radio es: Área = (5/2) * radio^2 * sin72°.
• Puedes dividir un pentágono regular en cinco triángulos congruentes para facilitar el cálculo del área.
• Calcular el área de un pentágono regular es útil en campos como la ingeniería, la arquitectura y el diseño.

Entendiendo el Pentágono Regular

Definición y Propiedades

Un pentágono regular es un polígono de cinco lados iguales y cinco ángulos iguales. Cada ángulo interior de un pentágono regular mide 108 grados.

Elementos Clave del Pentágono

• Lado: La longitud de uno de los lados del pentágono.
• Apotema: La distancia perpendicular desde el centro del pentágono hasta uno de sus lados.
• Radio: La distancia desde el centro del pentágono hasta uno de sus vértices.

Métodos para Calcular el Área

1. Usando el Lado y el Apotema

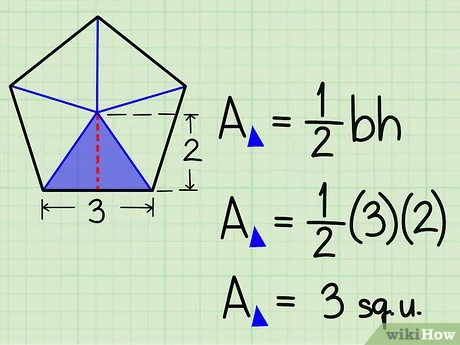
Este método es uno de los más intuitivos para calcular el área de un pentágono regular. Se basa en la idea de dividir el pentágono en cinco triángulos congruentes:

1. Divide el pentágono en cinco triángulos: Dibuja líneas desde el centro del pentágono hasta cada uno de sus vértices, creando cinco triángulos congruentes.
2. Identifica la base y la altura: Cada triángulo tiene como base un lado del pentágono y como altura el apotema.
3. Calcula el área de un triángulo: Usa la fórmula del área del triángulo: Área = (1/2) * base * altura.
4. Multiplica por cinco: El área del pentágono es la suma de las áreas de los cinco triángulos, por lo que multiplicas el área de un triángulo por cinco.

Fórmula: Área = (5 * lado * apotema) / 2

2. Usando Solo el Lado

Si solo conoces la longitud del lado del pentágono, puedes utilizar la trigonometría para calcular el área.

1. Divide el pentágono en cinco triángulos y luego divide uno en dos triángulos rectángulos: El ángulo en la parte superior del triángulo rectángulo siempre es de 36°.
2. Usa la trigonometría para encontrar la altura: tan36° = base/altura. La base es la mitad de la longitud del lado del pentágono.
3. Calcula el área del triángulo más grande: Área = (1/2) * base * altura.
4. Multiplica por cinco: El área del pentágono es la suma de las áreas de los cinco triángulos, por lo que multiplicas el área de un triángulo por cinco.

Fórmula: Área = (5 * lado^2) / (4 * tan36°)

3. Usando Solo el Radio

Si solo conoces el radio del pentágono, puedes usar la siguiente fórmula:

Fórmula: Área = (5/2) * radio^2 * sin72°

Aplicaciones Prácticas

El cálculo del área de un pentágono regular tiene aplicaciones en diversas áreas:

• Arquitectura: Los pentágonos regulares se utilizan en el diseño de edificios, estructuras y patios.
• Ingeniería: Los pentágonos se utilizan en el diseño de puentes, torres y otras estructuras.
• Diseño: Los pentágonos regulares se usan en el diseño de logotipos, patrones y otros elementos visuales.

Video Recomendado: Cómo calcular el área de un pentágono regular: Una guía completa

Preguntas Frecuentes

¿Cómo puedo encontrar el apotema de un pentágono regular?

Puedes encontrar el apotema de un pentágono regular utilizando la longitud del lado y la trigonometría. Dividiendo el pentágono en cinco triángulos congruentes, puedes enfocarte en uno de ellos. El apotema es la altura de este triángulo, que también es la distancia desde el centro del pentágono hasta el punto medio de uno de sus lados. Si conoces la longitud del lado, puedes utilizar la trigonometría para calcular el apotema.

¿Puedo calcular el área de un pentágono irregular?

No se puede usar la misma fórmula para calcular el área de un pentágono irregular. Para un pentágono irregular, necesitarías dividirlo en triángulos o utilizar métodos más avanzados de cálculo de área.

¿Existe una fórmula para calcular el perímetro de un pentágono regular?

Sí, la fórmula para calcular el perímetro de un pentágono regular es: Perímetro = 5 * lado.

¿Qué es un pentágono regular?

Un pentágono regular es un polígono de cinco lados iguales y cinco ángulos iguales. La suma de los ángulos interiores de un pentágono regular es 540 grados, lo que significa que cada ángulo interior mide 108 grados.

Conclusión

Calcular what is the area of the regular pentagon below es una habilidad útil en diversas áreas. Existen varios métodos para hacerlo, dependiendo de la información que se tenga disponible. Ya sea utilizando el lado y el apotema, solo el lado, o solo el radio, puedes encontrar el área de un pentágono regular con precisión. Recuerda aplicar las fórmulas correctas y las herramientas matemáticas para obtener resultados precisos. ¡Practica y explora las diferentes fórmulas para dominar el cálculo del área de un pentágono regular!

Si quieres conocer otros artículos parecidos a Cómo calcular el área de un pentágono regular: Una guía completa puedes visitar la categoría Educación.